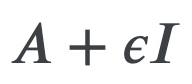
An explanation using Sard's Theorem.
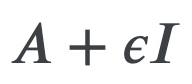
An explanation using Sard's Theorem.
The definitive graduate-level textbook on differential topology.


My personal plan to make 2023 the most productive year yet!

Covid really wrecked the bicycle supply chain.

An optimization algorithm for non-differentiable objective functions.

Check out my new course!
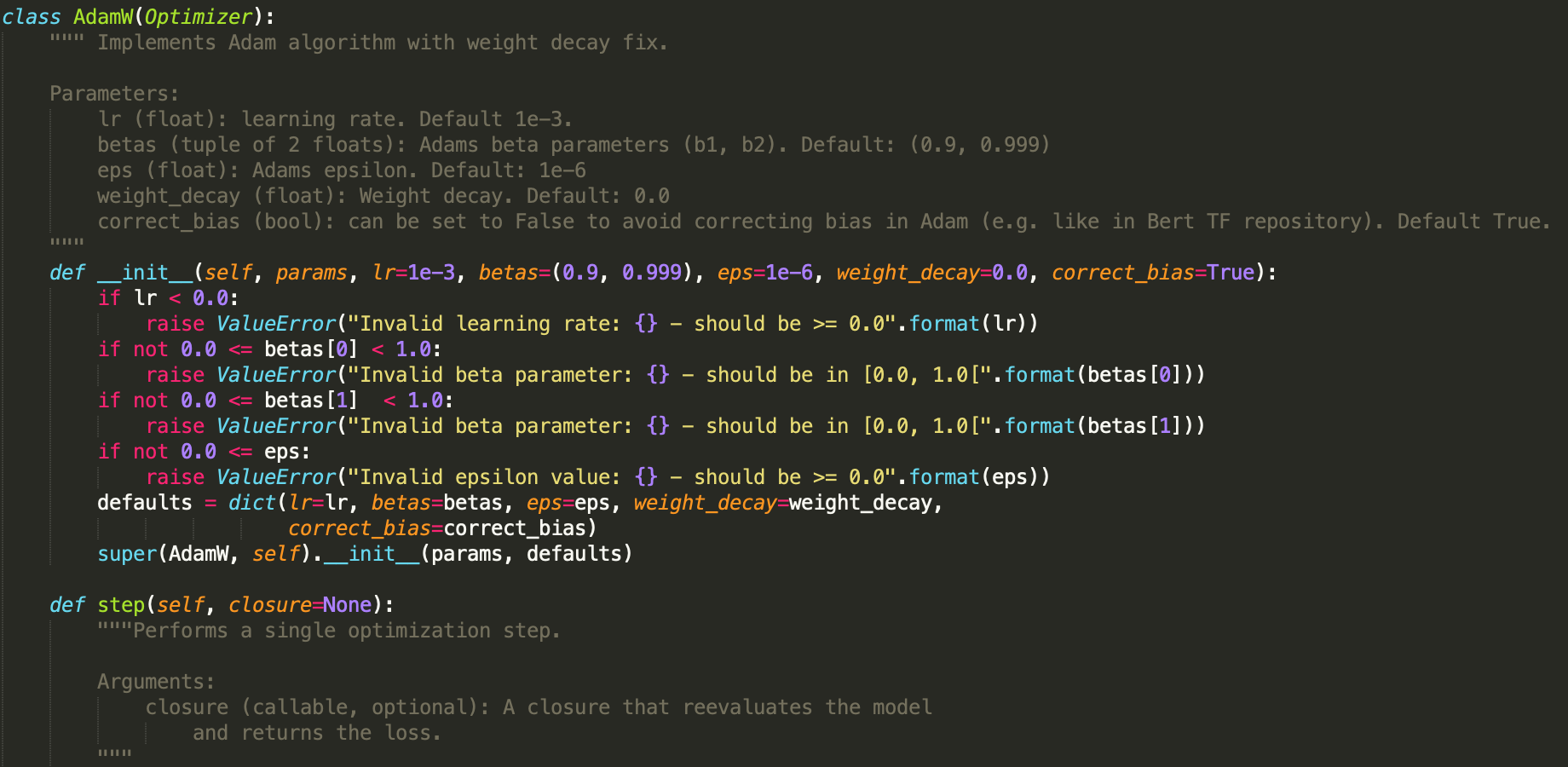
Write your own optimizers in PyTorch using these few simple steps.

A neural network can predict which movies are most likely to become hits at the box office!
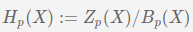
Homology gives a way to categorize topological spaces.

Techniques for improving the performance of policy gradient methods.
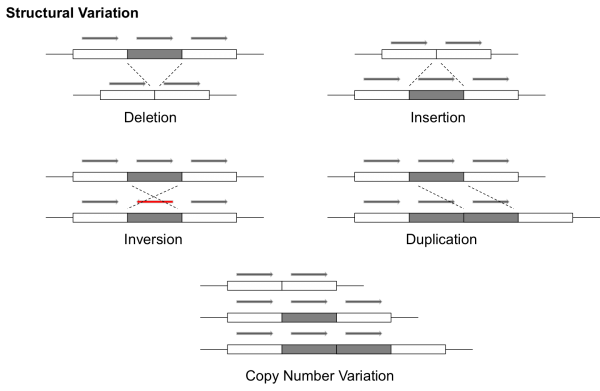
Identifying variants in genomic sequences and an introduction to Google's DeepVariant model.

A manifold is a structure

This theorem guarantees the existence of fixed points in complete metric spaces under a contraction mapping.

The REINFORCE Algorithm
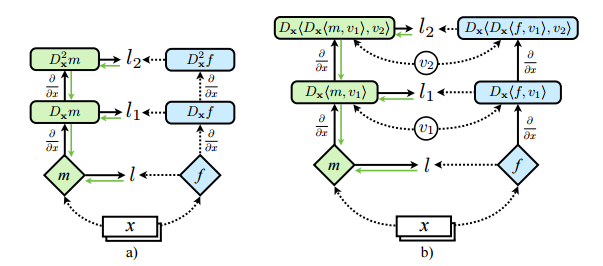
Take a neural network and achieve better results by training to not only optimize function values, but derivative values as well.
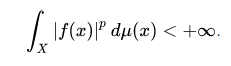
Normed Vector Spaces
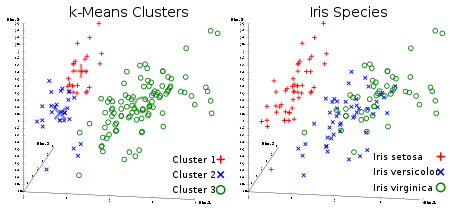
k-means is an unsupervised clustering algorithm.
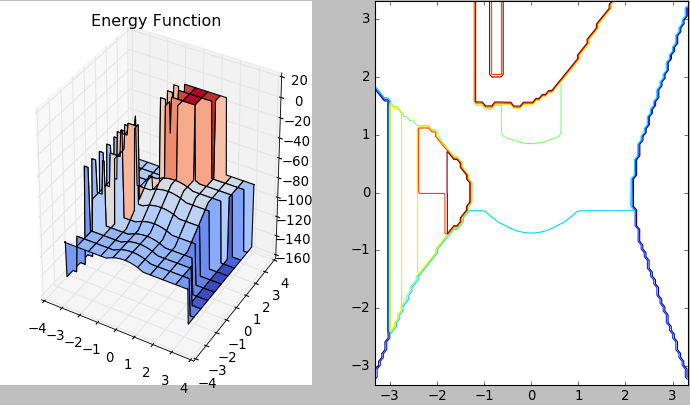
Hopfield Networks are unique in that they possess a primitive, internal memory storage system.
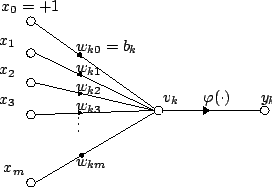
We can use the McCulloch-Pitts model of a neuron to compute any logical function.
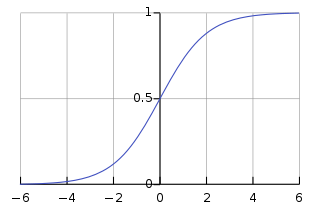
Logistic Regression is a discriminative model for classification which seeks to model the class posterior probabilities.
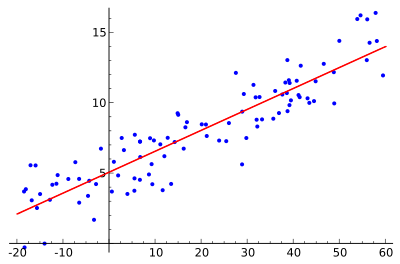
In this tutorial we use linear regression to complete a binary classification task.
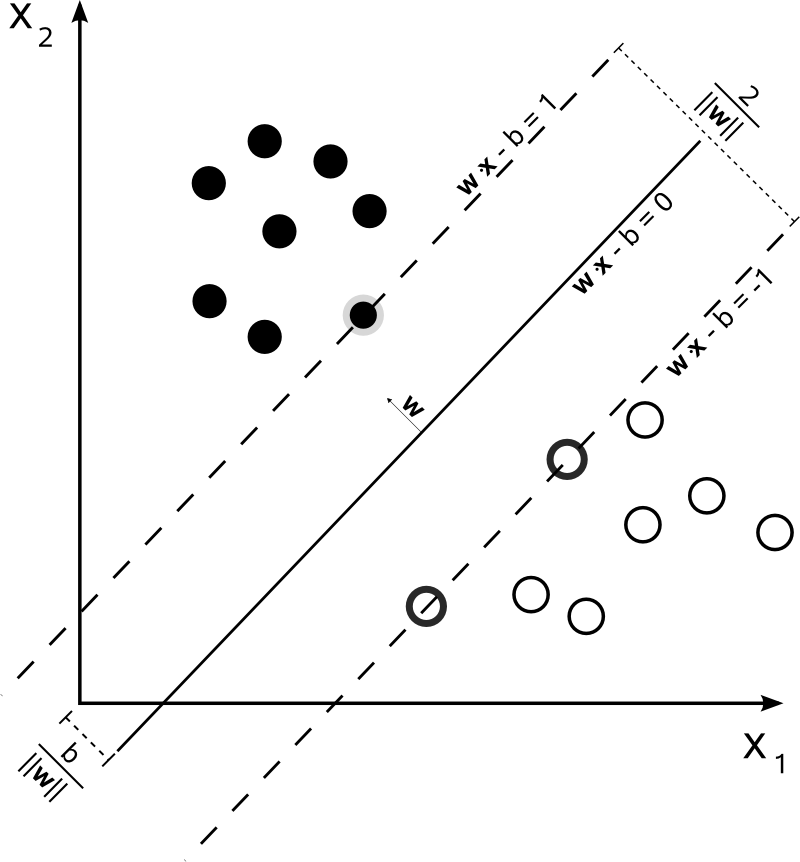
The support vector machine is a kernelized classification algorithm.
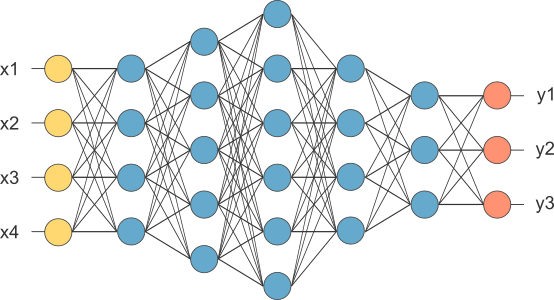
A discriminative model for classification.

Any continuous function can be approximated to an arbitrary degree of accuracy by some neural network.
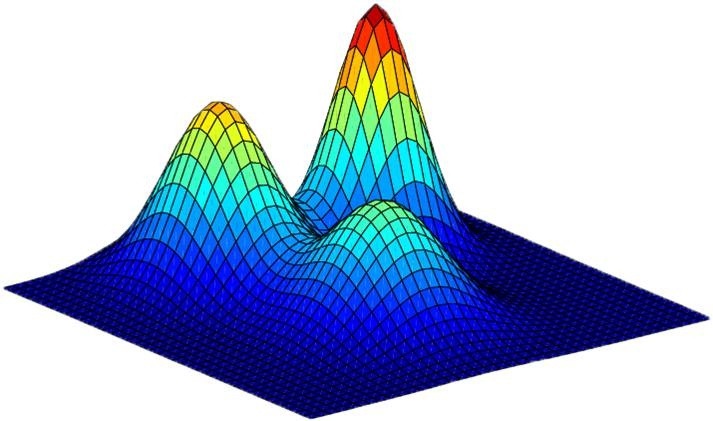
Mixing Gaussians without the help of a blender.
Often in mathematics, it is useful to be able to compute an approximation to a given function \(f(x)\). One way of doing this is to find some \(a\) for which \(f(x)\) is easy to compute. We can then calculate the approximate value of \(f(x)\) when \(x\) is near \(a\). We will call this approximation \(f_{a}(x)\). More concretely, we might say \(x\) is near \(a\) when \(\left|x - a\right| < \varepsilon\) for some threshold value of \(\varepsilon\) our choosing. One way of settling upon such an \(\varepsilon\) might be by determining an acceptable upper bound \(U\) on the error of our approximation \(\left|f(x) - f_{a}(x)\right|\) and then finding the greatest \(\varepsilon\) such that: \[\left|f(x) - f_{a}(x)\right| < U \quad \forall x \in (a - \varepsilon,\ a + \varepsilon)\]
Exercises from Chapter 1 of the book.

Exercise 1: If \(r\) is rational (\(r \neq 0\)) and \(x\) is irrational, prove that \(r + x\) and \(rx\) are irrational.
Suppose \(r \in \mathbb{Q}\) and \(x \in \mathbb{I}\) but \(r+x,\ rx \in \mathbb{Q}\). Then we have \(r +x = \frac{a}{b}\) for some \(a,b \in \mathbb{Z}\). This implies that \(x = \frac{a}{b} - r\). Since \(r \in \mathbb{Q}\), \(r = \frac{c}{d}\) for some \(c, d \in \mathbb{Z}\). Therefore \[x = \frac{a}{b} - \frac{c}{d} = \frac{ad-bc}{bd}\] which implies \(x \in \mathbb{Q}\): a contradiction. Therefore, \(r + x\) is irrational. Now, consider \(rx\). If \(rx \in \mathbb{Q}\), then
\begin{align}
rx &= \frac{a}{b}\ \text{for}\ a,b \in \mathbb{Z}
\implies x &= \frac{a}{b} \cdot \frac{d}{c}
\implies x &\in \mathbb{Q}
\end{align}
which is a contradiction. Therefore, \(rx\) is irrational.