What's in a Differential Form? - Part 1

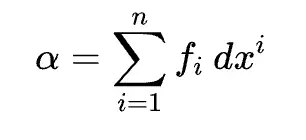
In my opinion, one of the reasons that differential forms are so confusing to new students is that the pedagogy in introductory calculus classes is often insufficiently rigorous. For example, in a first course in calculus, students are taught to integrate single variable functions and are instructed to think of this operation as computing the area under a curve. In multivariable calculus, one is introduced to other notions of an integral, such as the line integral in which one integrates a function over a curve. Yet, instructors fail to emphasize how these different variants of integration are related.

In fact, there are two fundamentally distinguishable types of integration.

First, the unsigned integral is used to compute quantities that are exclusively non-negative, such as the mass of an object of varying density or the probability of an event occuring. In particular, unsigned integrals are taken over sets. A set does not have a direction; more precisely, it does not have an orientation, so there is no ambiguity in how to integrate over it. The unsigned integral obtains its full generality in the Lebesgue integral of measure theory. With Lebesgue integration, we assign sets a measure, which is a generalization of the notion of “size” or “volume,” and then we integrate over these sets.

Yet, there are many instances where we do want to incorporate some notion of direction or orientation into our integration. This leads us to consider the notion of a signed integral, which takes orientation into account. For example, we would want to consider sign when computing the work done by a force along a path or the flux of a

Another reason for the confusion of the different types of integration is a common abuse of notation. Take as an example the integral of a function $f(x): \mathbb{R} \to \mathbb{R}$ over an interval $[a, b]$. In calculus, we are taught to write this integral as $$\int_a^b f(x)\ dx.$$ However, we are also shown that we can change the sign of the integral by swapping the limits of integration, i.e. $$\int_a^b f(x)\ dx = -\int_b^a f(x)\ dx.$$ In fact, this is just shorthand for integrating the 1-form, $f(x)\ dx$, over the interval $[a, b]$, i.e. $$\int_{[a, b]}f(x)\ dx = \int_a^b f(x)\ dx.$$ and the version with the limits of integration swapped amounts to integrating the 1-form, $-f(x)\ dx$, over $[a, b]$, i.e. $$\int_{[a, b]} -f(x)\ dx = -\int_b^a f(x)\ dx.$$

In measure theory, where the unsigned integral is the primary player, we write this integral as $$\int_{[a, b]} f(x)\ d\mu.$$ where $\mu$ is the Lebesgue measure of $[a, b]$. We might also write this as $$\int_{[a, b]} f(x)\ |dx|$$ where we are being more explicit that $dx$ is an object that takes into account orientation and that we are effectively removing consideration of this orientation by taking the absolute value, thereby turning it into a measure.

Revisiting the Derivative

Almost everyone is familiar with the definition of the derivative of a scalar function $f: \mathbb{R} \to \mathbb{R}$. $$f’(x) = \lim_{h \to 0} \frac{f(x + h) - f(x)}{h}$$

However, there are multiple definitions of a “derivative” in higher dimensions. Perhaps the most common is that of the directional derivative¹. Given a function $f: U \to \mathbb{R}^m$, where $U$ is an open subset of $\mathbb{R}^m$, the directional derivative is defined as $$(Df)_{\mathbf{x}}(\mathbf{v}) = \lim_{h \to 0} \frac{f(\mathbf{x} + h\mathbf{v}) - f(\mathbf{x})}{h}$$ where $v$ is a vector in $\mathbb{R}^n$. We use the notation $(Df)_{\mathbf{x}}(\mathbf{v})$ to emphasize that the derivative is taken at the point $\mathbf{x}$ in the direction of $\mathbf{v}$. This notation also emphasizes that there is a more complete quantity, the total derivative² $Df$ of $f$, which is being evaluated in the direction of the vector $\mathbf{v}$.

The total derivative of a function $f: U \to \mathbb{R}^m$ is defined as the linear transformation $D: \mathbb{R}^n \to \mathbb{R}^m$ satisfying $$f(x + v) = f(x) + D(v) + R(v)$$ where $R(v)$ is a remainder function satisfying $\lim_{|v| \to 0} \frac{R(v)}{|v|} = 0$. The total derivative is a natural consequence of Taylor’s theorem, which states that a function can be approximated by its value at $x$ plus a linear term plus a remainder that encompases higher-order terms that are at least quadratic in $v$.

The total derivative $D$ is the linear part of $f$ at $x$. In one dimension, the total derivative is just the scalar derivative $f’(x)$, and the linear transformation $D: \mathbb{R} \to \mathbb{R}$ is just multiplication by $f’(x)$. On manifolds, the total derivative is sometimes called the differential of $f$ and is denoted $df$. If $f: M \to N$ where $M$ and $N$ are manifolds, then at any point $x \in M$, $df_x: T_xM \to T_xN$ is a map from the tangent space of $M$ at $x$ to the tangent space of $N$ at $f(x)$.

In the special case where $N = \mathbb{R}$, the tangent space $T_{f(x)}N$ is just $T_{f(x)}\mathbb{R} \cong \mathbb{R}$, and in this case the differential is a linear functional on the tangent space, $T_xM$. We call the space of linear functionals on $T_xM$ the cotangent space and denote it $T^\ast_xM$. For this reason, linear functions $\omega_p : T_pM \to \mathbb{R}$ are also sometimes called covectors. The differential $df_x$ is one such element of the cotangent space at $x$ and thus a covector. Taking the disjoint union over all the cotangent spaces of $M$ gives the cotangent bundle $$T^\ast M = \bigsqcup_{x \in M}T^\ast_x M$$ of $M$. Given this structure, we can then define a differential 1-form as a section of the cotangent bundle. More simply, a differential 1-form is a covector field $\omega$ on $M$, i.e. an assignment of a covector $\omega_p$ to every point $p \in M$.

The Differential in Coordinates

It’s helpful for understanding the differential to assign coordinates to some open $U \subset M$. Let $(x^1, \ldots, x^n)$ be some such coordinates. Then, $\left(\frac{\partial}{\partial x^1}, \ldots, \frac{\partial}{\partial x^n}\right)$ is a basis for the tangent space $T_pM$ at any point $p \in U$. The cotangent space also has a basis, and the basis vectors are themselves differential 1-forms. They are typically denoted $(dx^1, \ldots, dx^n)$, and they act on a vector $v \in T_pM$, $$v = \sum_i v^i \frac{\partial}{\partial x^i}\bigg|_p$$ by picking out the $i$th component of $v$, i.e. $$(dx^i)_p(v) = v^i.$$ Thus, every 1-form $\omega$ on $U$ can be written as $$\omega = \sum_i a_i dx^i$$ In particular, for a $C^{\infty}$ function $f: U \to \mathbb{R}$, we have $$df = \sum_i a_i dx^i.$$ To find $a_i$, we evaluate $df$ on any of the basis vectors of $T_pM$, $$df\left(\frac{\partial}{\partial x^j}\right) = \sum_i a_i dx^i\left(\frac{\partial}{\partial x^j}\right) \implies \frac{\partial f}{\partial x^j} = \sum_i a_i \delta_j^i = a_j.$$ Thus, the local expression for $df$ in coordinates is $$df = \sum_i \frac{\partial f}{\partial x^i} dx^i.$$

Let’s note something here. Suppose $M$ is three-dimensional. Then in coordinates, $df$ can be written as

Diving into Duality

We’ve already looked at how covectors are dual to tangent vectors and vice versa. The same idea extends to vector fields and covector fields (i.e. differential 1-forms).

Given a one-form $\omega$ written as $$\omega = f\ dx + g\ dy + h\ dz,$$ the vector field $\mathbf{F}$ dual to $\omega$ is defined by $$\mathbf{F} = f \frac{\partial}{\partial x} + g \frac{\partial}{\partial y} + h \frac{\partial}{\partial z} = (f, g, h)$$ and vice versa.

Pullbacks and All That

Now, suppose $F: M \to N$ is a smooth map between smooth manifolds. Of course, the differential of $F$ is a map $dF_p: T_pM \to T_{F(p)}N$. There is a dual linear map $$dF^\ast: T^\ast_{F(p)}N \to T^\ast_pM$$ called the pullback by $F$ at $p$. The pullback takes 1-forms on the cotangent space of $N$ at $F(p)$ and sends them to 1-forms on the cotangent space of $M$ at $p$. The map is defined by its action on $\omega \in T^\ast_{F(p)}N$ and $v \in T_pM$, as $$dF_p^\ast(\omega)(v) = \omega(dF_p(v)).$$

Helpful References

1. Differential Forms and Integration by Terence Tao.
2. One-Forms and Vector Fields by Vincent Bouchard.
3. The De-Rham Complex on $\mathbb{R}^n$ by Loring Tu.
4. Differential Forms by Victor Guillemin and Peter J. Haine.
5. An Introduction to Manifolds by Loring Tu.

Footnotes