Introduction to Smooth Manifolds -- Some Solutions
The definitive graduate-level textbook on differential topology.
A manifold is a structure
This theorem guarantees the existence of fixed points in complete metric spaces under a contraction mapping.
The REINFORCE Algorithm
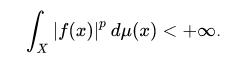
Normed Vector Spaces
Often in mathematics, it is useful to be able to compute an approximation to a given function \(f(x)\). One way of doing this is to find some \(a\) for which \(f(x)\) is easy to compute. We can then calculate the approximate value of \(f(x)\) when \(x\) is near \(a\). We will call this approximation \(f_{a}(x)\). More concretely, we might say \(x\) is near \(a\) when \(\left|x - a\right| < \varepsilon\) for some threshold value of \(\varepsilon\) our choosing. One way of settling upon such an \(\varepsilon\) might be by determining an acceptable upper bound \(U\) on the error of our approximation \(\left|f(x) - f_{a}(x)\right|\) and then finding the greatest \(\varepsilon\) such that: \[\left|f(x) - f_{a}(x)\right| < U \quad \forall x \in (a - \varepsilon,\ a + \varepsilon)\]
Solutions to Rudin's Principles of Mathematical Analysis
Exercises from Chapter 1 of the book.
Exercise 1: If \(r\) is rational (\(r \neq 0\)) and \(x\) is irrational, prove that \(r + x\) and \(rx\) are irrational.
Suppose \(r \in \mathbb{Q}\) and \(x \in \mathbb{I}\) but \(r+x,\ rx \in \mathbb{Q}\). Then we have \(r +x = \frac{a}{b}\) for some \(a,b \in \mathbb{Z}\). This implies that \(x = \frac{a}{b} - r\). Since \(r \in \mathbb{Q}\), \(r = \frac{c}{d}\) for some \(c, d \in \mathbb{Z}\). Therefore \[x = \frac{a}{b} - \frac{c}{d} = \frac{ad-bc}{bd}\] which implies \(x \in \mathbb{Q}\): a contradiction. Therefore, \(r + x\) is irrational. Now, consider \(rx\). If \(rx \in \mathbb{Q}\), then
\begin{align}
rx &= \frac{a}{b}\ \text{for}\ a,b \in \mathbb{Z}
\implies x &= \frac{a}{b} \cdot \frac{d}{c}
\implies x &\in \mathbb{Q}
\end{align}
which is a contradiction. Therefore, \(rx\) is irrational.